Между идентификаторами множеств можно использовать логические операторы взаимодействия. По сути это влияет на итоговый набор фильтров, применяющихся в выражении:
- Объединение (+): объединяет выборки из множеств;
- Исключение (-): исключает из одной выборки значения другой выборки;
- Пересечение (*): оставляет только те значения, которые пересекаются в обеих выборках;
- Исключение пересечения (/): оставляет значения, не пересекающиеся в обеих выборках.
Создайте новый лист в приложении. Разместите на нем блок с фильтрами, и таблицу. В таблицу добавьте:
- Измерение Категория;
- Меру sum(Sales);
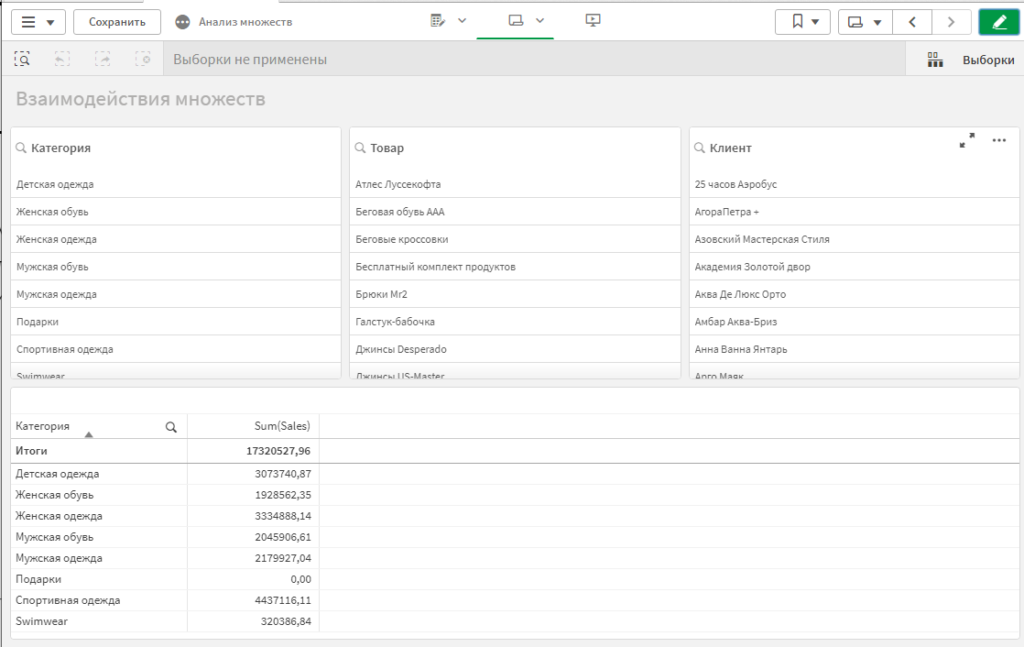
Для вызуализации примера с вузаимодействиями множеств, нам нужно создать 2 закладки:
Выберите в измерении Категория значения: Детская одежда, Женская обувь, Женская одежда, Мужская обувь, Мужская одежда, и создайте закладку под названием BM1.
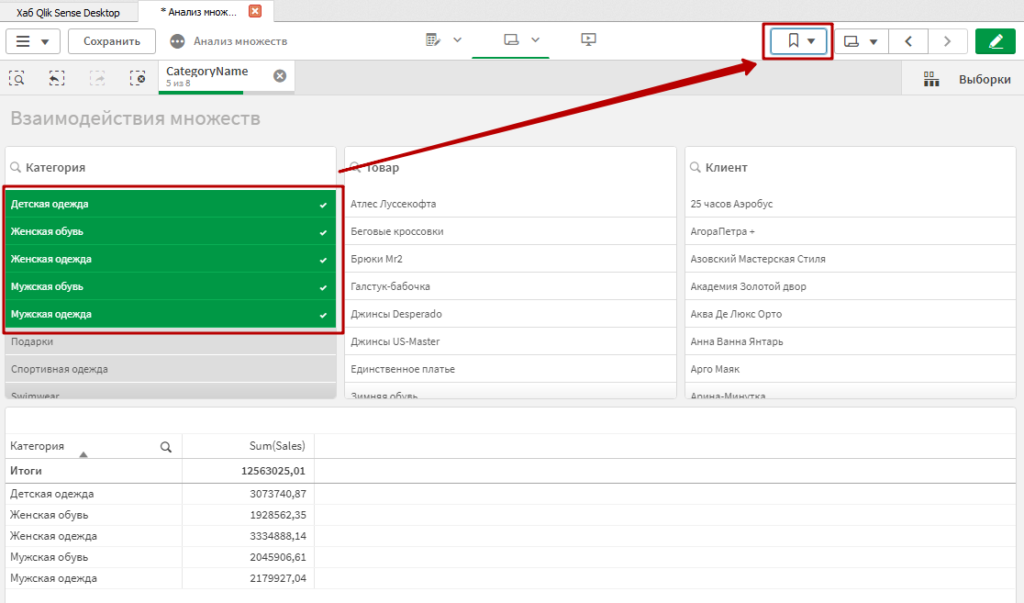
После этого повторите процесс, предварительно отобрав в фильтре Категория значения: Мужская обувь, Мужская одежда, Подарки, Спортивная одежда, Swimwear.
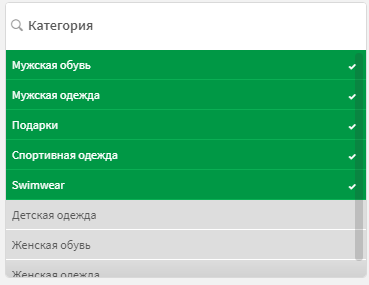
Сохраните этот отбор как закладку под названием BM2. Как вы могли заметить, у нас 2 закладки с разным набором категорий, из которых 2 пересекаются (Мужская обувь, Мужская одежда). Проверим на них взаимодействие множеств.
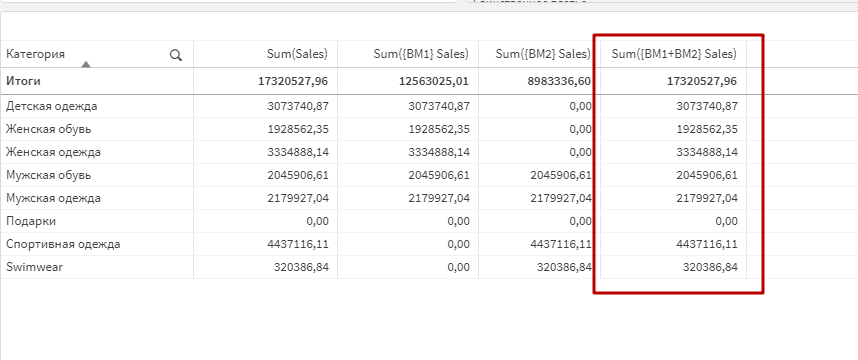
Создайте меры sum({BM1} Sales) и sum({BM2} Sales), чтобы увидеть, как они возвращают сумму продаж именно по сохраненным в закладках категориям.
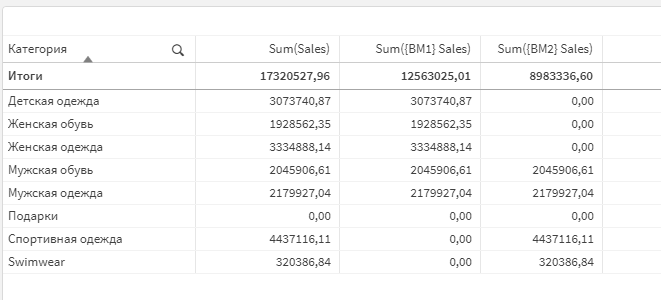
Создайте меру sum({BM1+BM2} Sales). Как видите, она возвращает сумму продаж по всем категориям. Здесь хорошо видно, что это не арифметическая операция, а логическая — итоговая сумма по этому выражению не является суммой выражений sum({BM1} Sales) и sum({BM2} Sales), иначе результат был бы равен 21 546 361, а не 17 320 527 . Мы имеем дело именно с полной комбинацией фильтров из обоих множеств.
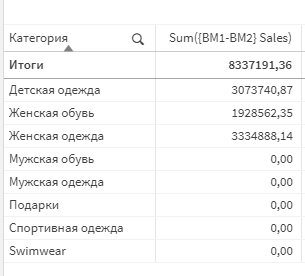
Теперь попробуем выражение sum({BM1-BM2} Sales). Как результат, из множества BM1 убираются значения, содержащиеся в множестве BM2. Это заметно на примерах общих категорий — Мужской обвуви и Мужской одежды.
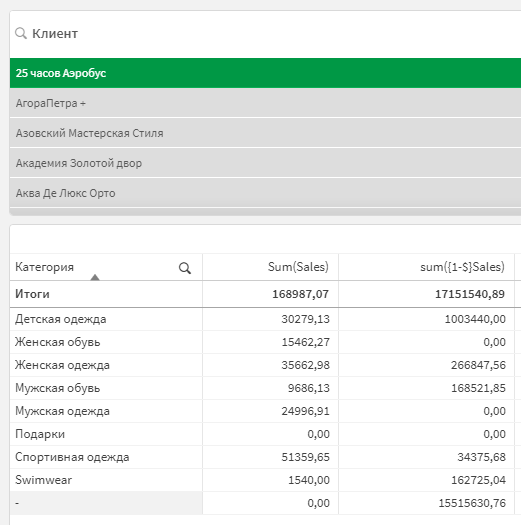
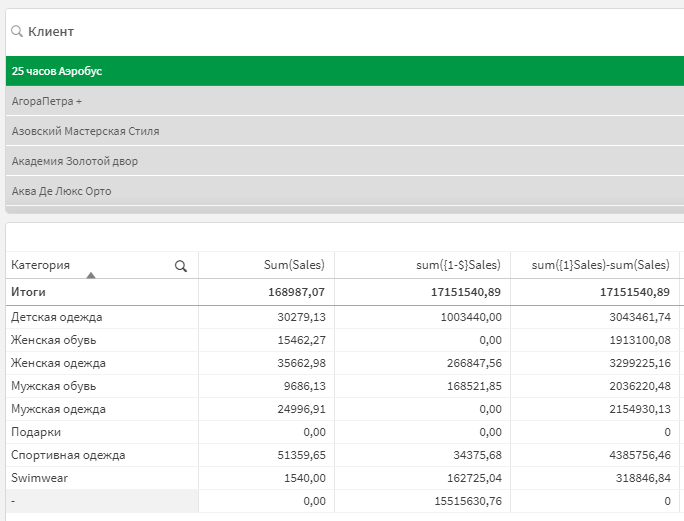
У исключения множеств есть подводный камень — его поведение будет зависеть от модели данных. Например, у вас категории товара вынесены в отдельный справочник, и вы строите выражение выражение вида sum({1-$}Sales), которое должно возвращать сумму продаж, исключенную текущей выборкой.
На фильтре вы отбираете клиента, а сама визуализация разбита на категории. Вы ожидаете, что выражение sum({1-$}Sales) покажет вам сумму продаж по категориям у остальных клиентов, которых мы не выбрали. И оно покажет, только вот значительная часть суммы будет отнесена к пустому значению Категории.
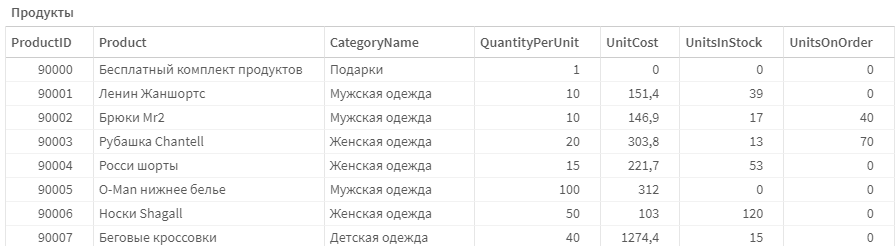
Это происходит из-за того, что в текущую выборку (продажи конкретного клиента) у нас попадает ряд товаров с категориями. И наименования этих товаров с категориями становятся исключенными для других клиентов, которые их покупали. Напомним, что справочник товаров у нас выглядит так:
Чтобы исправить ситуацию без переделывания модели данных, надежнее прибегнуть у формуле вида sum({1} Sales)-sum(Sales). Это позволит получить предсказуемое поведение визуализации, т.к. будет задействовано арифметическое вычитание, а не логическое исключение.
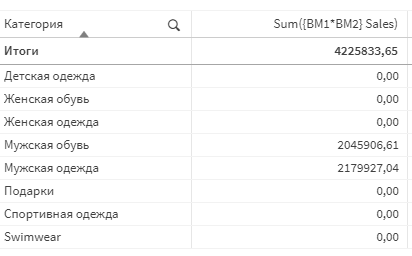
Пойдемте дальше. Выражение sum({BM1*BM2}Sales) вернет сумму продаж по пересекающимя значениям множеств. Т.е. по Мужской обуви и по Мужской одежде.
Выражение sum({BM1/BM2}Sales) вернет сумму продаж по не пересекающимя значениям множеств. Т.е. продажи по Мужской обуви и по Мужской одежде будут исключены.

Взаимодействия между множествами могут составлять полноценные выражения, со скобками для определяния порядка действий, и объединять системные множества, альтернативные состояния, и закладки.
На картике получается следующая логика формирования множества: Из всех данных исключается множество BM1, потом к результату добавляется множество BM2, и результат всего этого пересекается со множеством Excluded.

На самом деле, закладки как идентификатор множеств в реальных проектах используется крайне редко (у нас никогда не используется). Это скорее некоторая помощью для людей, которые не владеют синтаксисом модификаторов множеств (именно модификаторов, не идентификаторов). Но это мы исправим в следующем занятии.
А в качестве идентификаторов обычно используют альтернативные состояния, чтобы дать пользователю универсальный функционал выборок — когда пользователь может использовать любые наборы фильтров и взаимодействий между ними.